Д. Рауп, С. Стэнли. «Основы Палеонтологии»

Одна из причин, по которым промежуточные формы обычно причиняют не слишком много хлопот, состоит в том, что частота разных форм в животном и растительном мире неслучайна. Некоторые очертания встречаются чаще, другие — гораздо реже. Если система описательной терминологии верно отражает естественные группы преобладающих форм, то промежуточные случаи будут сравнительно редкими. Таким образом, разработка системы описательной терминологии уже сама по себе представляет значительный научный интерес, поскольку такая система призвана дать некую основную интерпретацию органического мира.

Конечно, есть опасность, что при разработке терминологии могут возникнуть ошибки и появиться неверные интерпретации. В палеонтологической литературе в прошлом неоднократно закреплялись многие совершенно непригодные системы описательной терминологии. Не соответствуя естественным группировкам, они мешали верному пониманию наблюдаемых фактов.

Описание посредством измерения

Заменяя описание с помощью специальной терминологии точными измерениями, мы избегаем некоторых трудностей, но вместо них тут же возникают новые. При достаточно точном измерении отпадает проблема промежуточных форм. Кроме того, данные измерений пригодны для ввода в ЭВМ, т. е. для непосредственной и эффективной обработки. Применение количественных данных пользуется хорошей репутацией среди ученых. Обычно считают, что только количественный подход по-настоящему объективен. Однако на самом деле измерения часто оказываются самым субъективным методом описания.

Рассмотрим пример (фиг. 12). Длина и высота раковины двустворчатого моллюска определяются линейными размерами.

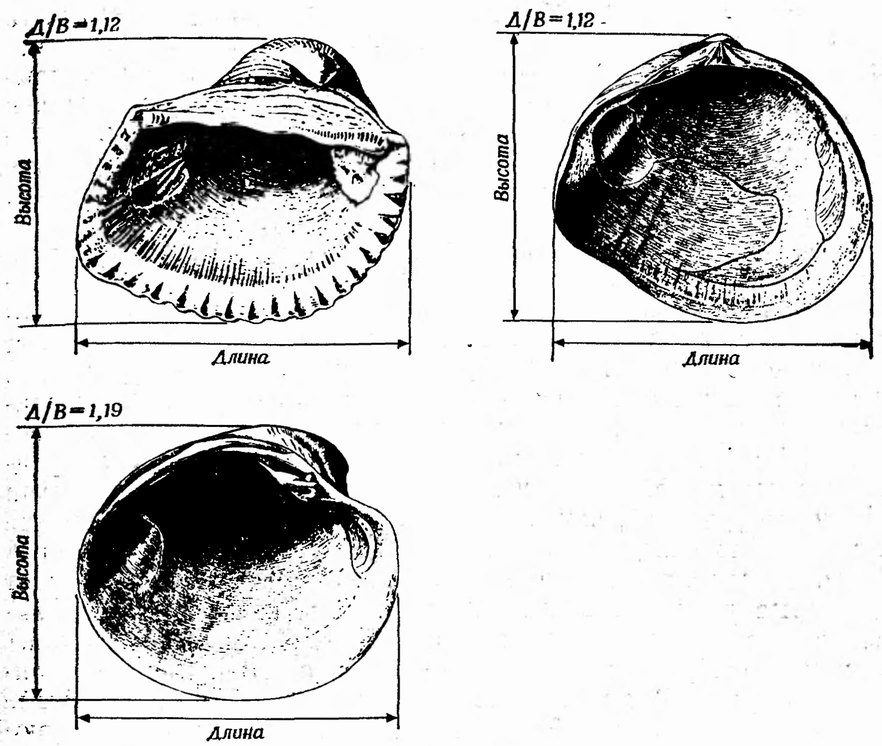
Фиг. 12. Внутренняя сторона створок трех видов двустворчатых моллюсков. Для всех трех форм соотношение выбранных нами главных параметров — длины и высоты — почти одинаково

Длина — максимальный линейный размер в передне-заднем направлении. Высота — максимальный размер, перпендикулярный длине. Эти данные содержат довольно много информации. Они говорят не только о размере раковины, но и о ее форме. Отношение длины к высоте — показатель формы. У равносторонних раковин это отношение приближается к единице. У удлиненных оно больше единицы.

Раковины трех двустворчатых моллюсков, показанные на фиг. 12, характеризуются почти одинаковым отношением длины к высоте, но даже ребенок заметит явные различия между этими экземплярами.

Здесь мы сталкиваемся с одним из самых крупных недостатков системы описания, основанной исключительно на измерениях. Явные различия в очертаниях раковин не отражаются в отношении их длины к высоте. Выражая форму двумя промерами, сделанными перпендикулярно друг к другу, мы подразумеваем, что описываемый предмет имеет прямоугольные очертания.

Если бы все двустворчатые раковины были прямоугольными, то все было бы просто и измерения длины и высоты или их отношение исчерпывающе характеризовали бы форму. Важно помнить, что, когда мы хотим описать какую-либо форму с помощью ряда измерений, мы создаем модель этой формы, т. е. представляем себе некий идеальный геометрический прототип и можем наблюдать или измерять отличия реального экземпляра только по отношению к этой модельной форме.

На фиг. 13 изображены четыре гипотетические спирально свернутые раковины головоногих моллюсков. Для каждой из них указан наибольший диаметр d, по которому крупные формы отличаются от небольших. Но диаметр мало говорит нам о форме раковины. Подразумеваемая модель — окружность. В одну и ту же окружность можно вписать много разных спирально закрученных головоногих; следовательно, диаметр говорит нам главным образом о величине раковины. Формы, представленные на фиг. 13, лучше описываются двумя неравными радиусами (r₁ и r₂), начинающимися в морфологическом центре спирали. Отметим, что отношение этих радиусов для формы А больше, чем их отношение для формы Г, что, конечно, отражает некоторые различия в очертаниях двух раковин. (Кстати, заметим, что сумма двух радиусов несколько меньше диаметра.) Можно расширить использование радиусов для описания спиральных форм. Вот уже полтора столетия известно, что многие спиральные раковины беспозвоночных имеют форму, поддающуюся строгому математическому описанию. У спирально свернутых раковин головоногих моллюсков отношение радиусов, измеренных по ходу спирали через равные угловые интервалы, обычно сохраняется одинаковым. Это показано на фиг. 14: отношение двух противоположных радиусов остается постоянным. Помня это, вернемся к фиг. 13 и охарактеризуем каждую раковину отношением радиусов, разделенных половиной оборота. Используя этот метод описания, мы сможем различить три формы головоногих. Однако раковины Б и В нельзя различить путем сравнения отношений радиусов, хотя на рисунке ясно видно, что очертания этих раковин различны.

При описании посредством измерений обычно не так важны число и точность измерений, как верный выбор подлежащих измерению параметров. В раковине головоногих можно было бы найти еще массу доступных для измерения признаков, но, по-видимому, ни один другой набор измерений не будет таким экономным или прямо достигающим цели, как отношение радиусов (хотя надо помнить, что для различения раковин Б и В на фиг. 13 потребуются и другие измерения). В идеале при измерении следует производить отбор информации, т. е. использовать лишь часть информации, отраженной на фотографии, так что морфология изучаемого объекта при этом схематизируется и уцрощается. Насколько это полезно для каждого данного описания, целиком зависит от общих задач исследования и поставленных вопросов. Нет какого-то одного набора измерений, который лучше всего описывал бы данный организм. Но, как правило, для каждой группы ископаемых организмов есть основной набор измерений, принятый большинством палеонтологов. Например, измерения, принятые для головоногих, до некоторой степени произвольны, но они позволяют составить весьма верное представление об их морфологии. Принятый набор измерений может заменять описание с помощью терминологии.

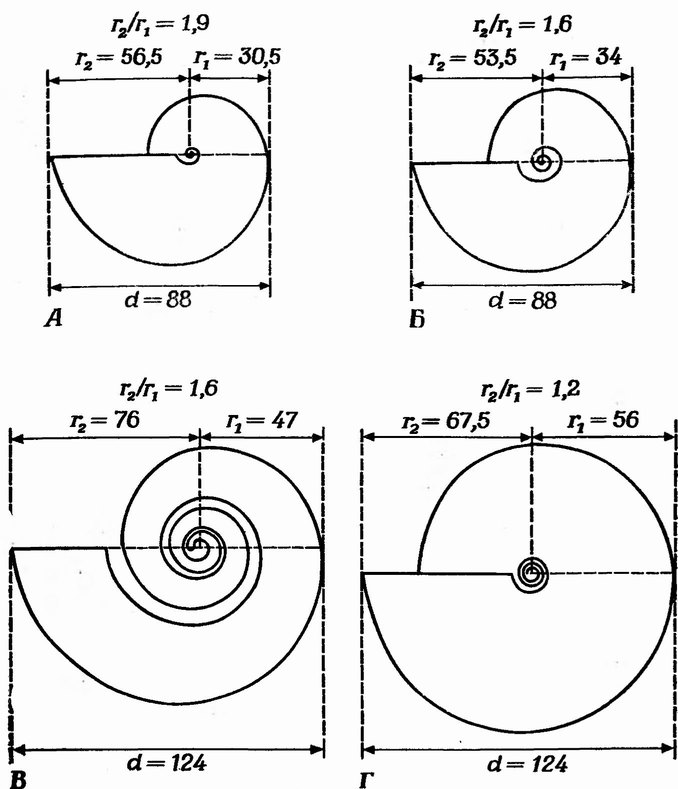
Фиг. 13. Четыре типа спирально свернутых раковин головоногих моллюсков (подробности в тексте)

Измерения можно применять для описания изменчивости особей. Располагая данными измерений большого числа особей, можно провести статистический анализ изменчивости.

После того как мы выбрали, что следует измерять, остаются еще две проблемы: какой метод измерения следует применить и к какой точности надо стремиться. До сих пор мы обсуждали только линейные размеры — кривые поверхности для измерения проецировались на плоскость. Проекция облегчает измерение и, как правило, допустима. Но она всегда связана с упрощением: кривая поверхность предполагается плоской. То же делается, когда для измерения расстояния между двумя точками кривой поверхности ископаемого применяется кронциркуль. Измерения, сделанные по фотографии, достаточно точны лишь в том случае, если плоскость фотографии совпадает с необходимой проекцией. Любое оптическое проецирование предмета (включая фотографирование) вносит определенные искажения, которые должны быть сведены к минимуму. Допустимая степень искажения зависит от требуемой точности и достоверности результатов.

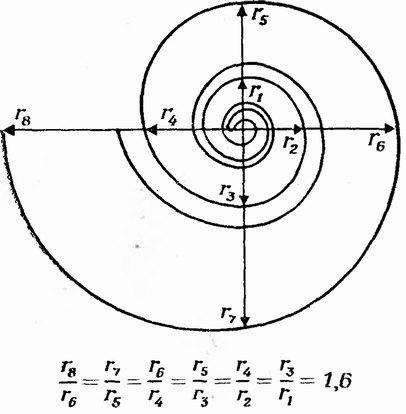
Фиг. 14. Обобщенная форма спирально свернутой раковины головоногого моллюска. На рисунке видно, что соотношение радиусов постоянно

Нет общих правил, помогающих выбрать степень точности измерений. Она целиком зависит от поставленной задачи исследования. Например, если мы хотим отличить трилобит от динозавра, достаточна точность измерений до метра. Точность до сантиметра или миллиметра в этом случае излишня. Но если нужно различить два очень сходных организма, необходима гораздо большая точность. Опытный работник добивается лишь той степени точности, какая нужна в данном конкретном случае.

Для измерения ископаемых придуманы различные приборы — сложные и простые. Многие из них сконструированы для узких целей. Так, инструмент, показанный на фиг. 15, изобретен в 1842 г. Альсидом д’Орбиньи для измерения так называемого апикального угла свернутых в коническую спираль раковин брюхоногих. Этот очень простой прибор состоит всего лишь из транспортира и линейки, но с успехом применяется для общего описания.

Для измерений часто применяется описанный ранее метод перевода морфологической информации в цифровую. Расстояние по прямой между двумя точками легко рассчитать, если известны координаты точек. Применение метода цифрового кодирования для единичных или немногочисленных измерений неоправданно. Но если нам нужно на каждой особи выполнить множество измерений, то цифровое кодирование и машинная обработка сильно облегчают задачу. Точность измерений, проводимых этим методом, целиком зависит от точности, с которой может быть определено положение точки в системе координат.

Фиг. 15. Инструмент для измерения вершинного угла раковин брюхоногих моллюсков, предложенный д'Орбиньи в 1842 г. [215]

<<   [1] ... [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] ...  [76]  >>