Д. Рауп, С. Стэнли. «Основы Палеонтологии»

Ископаемые организмы в этом отношении гораздо более перспективны. Во-первых, они более широко распространены (по крайней мере в осадочных породах). Во-вторых, их первоначальная форма, как правило, лучше известна и может быть определена с большей точностью (путем сравнения с недеформированными экземплярами тех же видов). В-третьих, первоначальная форма органических остатков обычно более сложна, и это обеспечивает получение более полных данных об имевших место деформациях. Достаточно просто могут быть определены первоначальный объем или размеры таких животных, как трилобиты, развитие которых сопровождается линькой и последовательные стадии роста которых морфологически различны. Если ископаемые сохраняются в породе в виде отпечатков, они изменяются во время деформации так же, как и сама вмещающая порода. Очень часто какая-либо неорганическая частица, например оолит, выдерживает большее напряжение, чем вмещающая порода; поэтому по деформации такой частицы не удается точно определить напряжение, приложенное ко всей породе.

Здесь мы будем рассматривать только двумерную деформацию, т. е. деформацию ископаемых, залегающих в плоскостях напластования. При этом мы ограничимся рассмотрением того, что геофизики называют «однородным напряжением», т. е. изменения объема и формы, при котором прямые линии остаются прямыми, параллельные — параллельными, а удлинения или укорочения первоначально одинакового направления имеют приблизительно одну и ту же величину.

В каждом примере мы будем сталкиваться с определением «эллипса деформации» — фигуры, которая получилась бы при действии тех же самых напряжений на круг. Наиболее важными характеристиками эллипса являются: направление большой оси (направление максимального удлинения), большая ось (величина максимального удлинения) и малая ось (величина минимального удлинения). Эти данные ничего не говорят о давлениях, вызывающих деформацию, потому что идентичные картины напряжения можно получить при весьма разнообразных системах давления. Например, данный эллипс деформации может быть получен растяжением, параллельным направлению максимального удлинения, или сжатием в перпендикулярном направлении.

На фото XXXVII показаны три деформированных хвостовых щита трилобитов. На фото XXXVII, А и Б деформация симметрична по отношению к первоначальной двусторонней симметрии трилобита; направление максимального удлинения параллельно оси двусторонней симметрии (Л) или перпендикулярно этой оси (Б). Если известна первоначальная морфология панциря трилобита, то можно определить направления максимального и минимального удлинения. Если же известно отношение основных размеров в недеформированном хвостовом щите, то можно вычислить отношение максимального удлинения к минимальному. Для того чтобы определить абсолютные значения удлинений, необходимо знать первоначальные размеры. Это возможно лишь в том случае, если изменчивость размеров раковин так незначительна, что ею можно пренебречь.

Фиг. 169. Влияние деформации на очертания двусторонне симметричных раковин брахиопод [155]. Первоначально все раковины имели одинаковые размеры

На фиг. 169 изображен более сложный пример двумерной деформации двусторонне симметричных ископаемых. Сравнивая представленные на ней деформированные и недеформированные раковины брахиопод, можно видеть, что расположение раковины по отношению к системе напряжений является решающим фактором. Обратите внимание, что деформированные экземпляры А и Б на фиг. 169 сравнимы соответственно с деформированными щитами Л и Б на фото XXXVII. Каждый из них параллелен или перпендикулярен направлению максимального удлинения. Все остальные образцы расположены под косым углом к направлению максимального удлинения и поэтому сравнимы со щитом B на фото XXXVII.

Фиг. 170. Определение эллипса деформации по изменению длины замочного края раковин брахиопод, изображенных на фиг. 169 [155]. Угол а — это угол между линией замочного края и прямой PQ (фиг. 169)

Существует несколько способов расчета деформаций, показанных на фиг. 169. В одном случае измеряемым морфологическим признаком каждого экземпляра является угол α, образуемый прямой, по которой измеряется длина замочного края h, и произвольной линией, проведенной через образцы (PQ). Результаты представлены графически на фиг. 170. Точки, соответствующие отдельным измерениям, достаточно хорошо укладываются на кривую, которая описывается следующим уравнением:

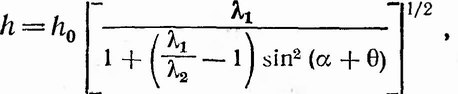
где h₀ — длина замочного края у недеформированного экземпляра, n — длина замочного края у деформированного образца, α — угол между замочным краем и произвольной линией PQ, θ — угол между линией PQ и направлением максимального удлинения (большая ось эллипса деформации), λ₁ и λ₂ — минимальное и максимальное удлинения.

На фиг. 170 точки хорошо ложатся на теоретическую кривую, что позволяет графически определить основные параметры эллипса деформации. Значение α в точке максимума кривой дает нам θ, а отношение ординат точек максимума и минимума кривой — отношение двух удлинений λ₁/λ₂. Таким образом, эллипс деформации можно определить, не зная точную морфологию недеформированных ископаемых и даже независимо от того, обладали ли ископаемые первоначально двусторонней симметрией. Важно, однако, иметь возможность допустить, что первоначально все ископаемые имели одинаковые размеры! Любая изменчивость образцов по размерам приводит к увеличению разброса точек, как это видно на фиг. 170. Если изменчивость слишком велика и если число экземпляров мало, то следует применять другие методы анализа.

Фиг. 171. Деформированные раковины брахиопод, иллюстрирующие влияние различной первоначальной ориентировки на деформацию [155]. Объяснения см. в тексте

На фиг. 171 изображены две деформированные раковины брахиопод разных видов. Для построения эллипса деформации нам достаточно знать, что обе раковины до деформации обладали двусторонней симметрией. Необходимо измерить три угла: угол (ψ) между первоначальной морфологически срединной линией и перпендикуляром к замочному краю (на каждом экземпляре) и угол (а) между замочными краями обоих экземпляров. Для отношения λ₁/λ₂ (задающего форму эллипса деформации) и угла 0 (ориентация длинной оси эллипса по отношению к одному из ископаемых) получаем следующие два уравнения:

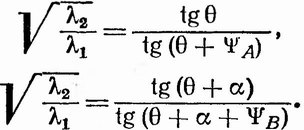
Для решения этих уравнений можно воспользоваться графическим методом (с помощью круга Мора).

На фиг. 172 схематически изображена створка раковины двустворчатого моллюска до и после деформации. Даже для раковины, не обладающей двусторонней симметрией, можно определить форму и ориентацию эллипса деформации, если известны углы между тремя линейными элементами раковины до и после деформации (показаны на фиг. 172 жирными линиями). Производим измерение двух углов (α и β). Величины R (R равно λ₁/λ₂) и θ (направление максимального удлинения по отношению к деформированному ископаемому) могут быть найдены путем совместного решения следующих двух уравнений:

Фиг. 172. Недеформированная (А) и деформированная (Б) раковины двустворчатых моллюсков [155]

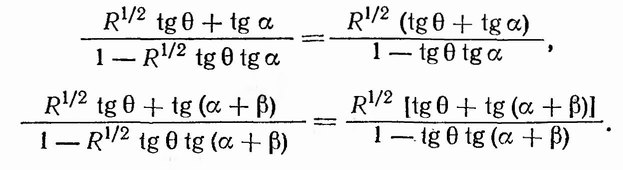
Как и в предыдущем случае, задача может быть решена графически.

Для более детального ознакомления с методами математического анализа деформации ископаемых органических остатков читателю следует обратиться к книге Рамсея [155]. Здесь мы ограничились лишь кратким и далеко не полным введением в эту область.

Рассмотренные примеры иллюстрируют важную роль ископаемых остатков в изучении деформаций осадочных пород. Эти примеры показывают также, что геофизик должен быть знаком с палеонтологией, а палеонтолог должен владеть методами геофизических исследований. Влияние деформации горных пород на форму ископаемых означает, что морфологическую изменчивость того или иного вида нельзя понять без учета возможных деформаций.

Реконструкция диагенетических обстановок

Изучение химического диагенеза требует знания минералогии, химического состава и структуры первоначального осадка. Без этих сведений геохимик может видеть лишь конечные продукты диагенеза. Многие известняки образуются главным образом из остатков скелетов морских беспозвоночных. Для ископаемых остатков организмов, у которых имеются близкие родичи среди ныне живущих видов, обычно удается довольно точно определить первоначальный скелетный материал. Таким образом, окаменелости часто служат ключом для восстановления процессов диагенеза.

<<   [1] ... [68] [69] [70] [71] [72] [73] [74] [75] [76]  >>